Girobicupolă triunghiulară alungită
| Girobicupolă triunghiulară alungită | |
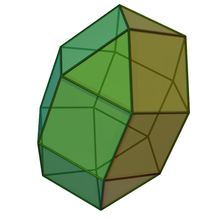 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J35 – J36 – J37 |
| Fețe | 20 (8 triunghiuri echilaterale, 12 pătrate)[1] |
| Laturi (muchii) | 36[1] |
| Vârfuri | 18[1] |
| χ | 2 |
| Configurația vârfului | 6 (3.4.3.4); 12 (3.43) |
| Grup de simetrie | D3d, [2+,6], (2*3), ordin 12 |
| Arie | ≈ 15,464 a2 (a = latura) |
| Volum | ≈ 4,955 a3 (a = latura) |
| Poliedru dual | – |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie girobicupola triunghiulară alungită este un poliedru convex construit prin alungirea unei girobicupole triunghiulare sau cuboctaedru, prin inserarea unei prisme hexagonale între cele două jumătăți, care sunt cupole triunghiulare (J3). Este poliedrul Johnson J36.[1][2] Rotirea uneia dintre cupole cu 60° înainte de alungire produce ortobicupola triunghiulară (J27), iar după alungire produce ortobicupola triunghiulară alungită (J35). Având 20 de fețe, este un tip de icosaedru. Deoarece această denumire se referă de obicei la icosaedrul regulat, rareori este folosită fără precizări suplimentare.
Mărimi asociate
[modificare | modificare sursă]Următoarele formule pentru arie, A și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Poliedre și faguri înrudiți
[modificare | modificare sursă]Girobicupola triunghiulară alungită formează faguri cu tetraedre și piramide pătrate.[3]
Note
[modificare | modificare sursă]- ^ a b c d e en Stephen Wolfram, "Elongated triangular orthobicupola" from Wolfram Alpha. Retrieved December 11, 2022.
- ^ en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603
- ^ en „J36 honeycomb”.


